Warning: Undefined variable $ext in /www/wwwroot/gkfeed.com/public_html/wp-content/plugins/show-hidecollapse-expand/bg_show_hide.php on line 281
Warning: Undefined variable $ext in /www/wwwroot/gkfeed.com/public_html/wp-content/plugins/show-hidecollapse-expand/bg_show_hide.php on line 281
Warning: Undefined variable $ext in /www/wwwroot/gkfeed.com/public_html/wp-content/plugins/show-hidecollapse-expand/bg_show_hide.php on line 281
Warning: Undefined variable $ext in /www/wwwroot/gkfeed.com/public_html/wp-content/plugins/show-hidecollapse-expand/bg_show_hide.php on line 281
Warning: Undefined variable $ext in /www/wwwroot/gkfeed.com/public_html/wp-content/plugins/show-hidecollapse-expand/bg_show_hide.php on line 281
6. A 40-foot tall arch with a parabolic shape has a line drawn between the bases of the two legs of the arch. If the height above the ground, y, of the arch can be written as the function y(x) = a(x – 20)(x + 20), where x represents the horizontal distance along the line between the bases from a point on the ground directly under the highest point of the arch, then what is the value of negative constant a ?
A. \( -\frac{1}{40} \)
B. \( -\frac{1}{20} \)
C. \( -\frac{1}{10} \)
D. -20
7. If 16a² + 4a – 6 = 0, what is a possible value of a ?
A. -0.75
B. -0.5
C. 0
D. 1
8. In order to make a profit, a zoo needs to sell at least 350 admission tickets each day. Four student groups, each of which includes 48 students, have purchased tickets for admission. If z represents the number of additional tickets sold today, and the zoo made its daily profit goal, which of the following inequalities could represent all possible values for z ?
A. 4(48) + z ≤ 350
B. 4(48) + z ≥ 350
C. 4(48) – z ≤ 350
D. 4(48) – z ≥ 350
9. A country’s birth rate is the number of births per year per 1,000 people in the country, and a country’s death rate is the number of deaths per year per 1,000 people. Immigration refers to the number of people who move into a country each year, and emigration refers to the number of people who move out of the country each year. A country’s population growth is determined by these four variables. Table 1 gives birth, death, immigration, and emigration rates in four countries and lines 1-4 in Figure 1 model the population for the four countries shown over time.
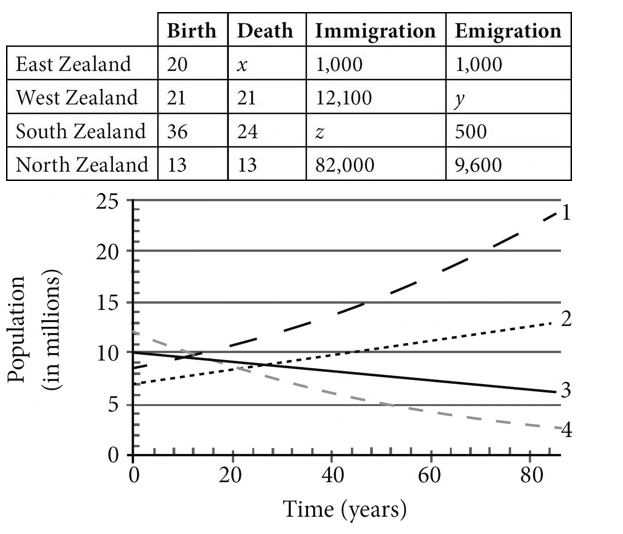
Line 1 represents which country’s population?
A. East Zealand
B. West Zealand
C. North Zealand
D. South Zealand
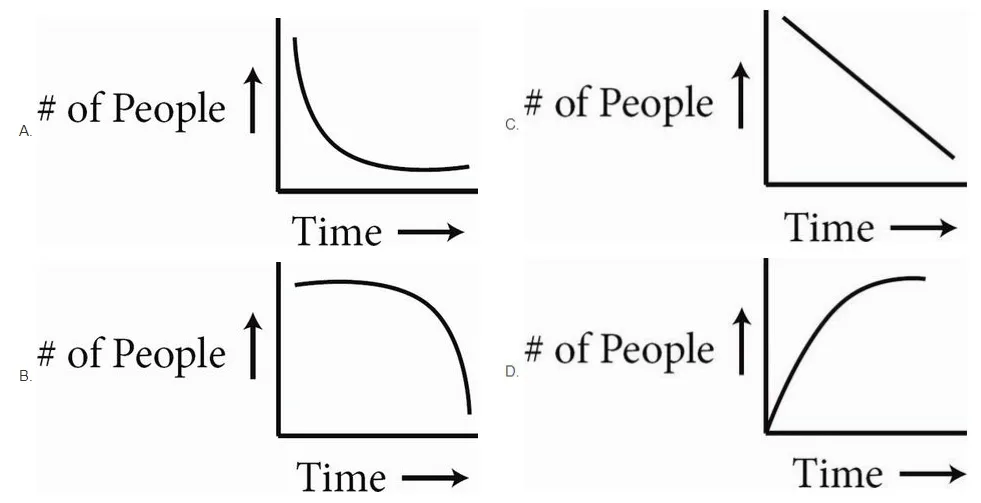
10. At the start of a new movie at the Cineplex 16, there are 250 people in the theater. However, 10% of the people walk out of the theater within the first 15 minutes of the movie starting. If another 10% leave in the next 15 minutes and this rate continues for the duration of the movie, which of the following graphs correctly models the number of people in the theater during the movie?
Warning: Undefined variable $in_same_cat in /www/wwwroot/gkfeed.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27
Warning: Undefined variable $excluded_categories in /www/wwwroot/gkfeed.com/public_html/wp-content/plugins/EXP.GKFEED.COM/function.php on line 27