The 2024 SAT standardized test is a critical assessment for college admissions. The math section covers a wide range of topics. To help students prepare, we’ve created a practice paper. This paper includes various math problems to help students become familiar with the test format and excel in their exam.
1. If the equation for a parabola is y = 5(x – 3)² – 3, which of the following points represents the parabola’s vertex?
A. (3, -3)
B. (3, 0)
C. (0, -3)
D. (-3, 3)
2.
\[ \frac{3}{c+2}(c+2)=(5-\frac{c}{c+2})(c+2) \]
In the equation above, what is the value of c ?
A. -4
B. \( -\frac{7}{4} \)
C. \( -\frac{7}{5} \)
D. \( \frac{1}{5} \)
3.
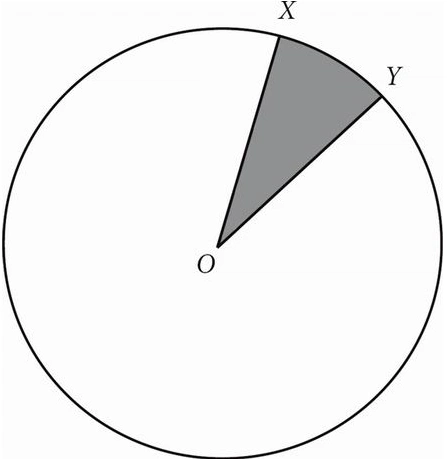
In the figure above, O is the center of the circle and the diameter is 10. If the area of the shaded region is π, what is the length of minor arc XY ?
A. \( \frac{2π}{5} \)
B. \( \frac{4π}{5} \)
C. \( \frac{5π}{2} \)
D. 5π
4.
x + 3y = 42
3x – y = 8
In the system of equations above, how many points of intersection do the equations share and what is their relationship, if any?
A. Zero, and the lines are parallel.
B. Infinitely many, and the lines are the same line.
C. One, and the lines have no relationship.
D. One, and the lines are perpendicular.
5.
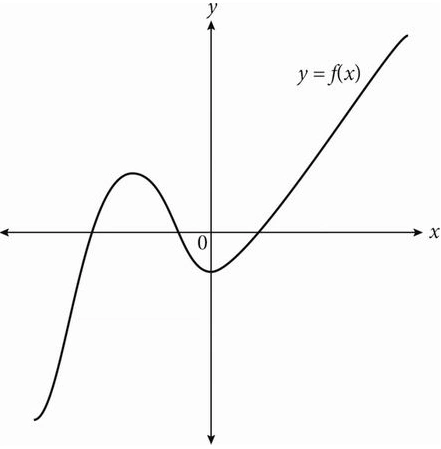
The figure above shows the graph in the xy-plane of the function f. If q, r, s and t are distinct real numbers, which of the following could be f(x) ?
A. f(x) = (x – q)²
B. f(x) = (x – r)(x + s)
C. f(x) = (x – r)(x + s)(x + t)
D. f(x) = (x – q)(x – r)(x + s)(x + t)