The 2024 SAT standardized test is a critical assessment for college admissions. The math section covers a wide range of topics. To help students prepare, we’ve created a practice paper. This paper includes various math problems to help students become familiar with the test format and excel in their exam.
1. Y=\( \frac{A}{A+W} \)
A gardener prepares a mixture of fertilizer with concentration, by volume, equal to Y. It is prepared by mixing a volume of fertilizer given by A with a volume of water given by W. The expression above represents the mixture described. What physical quantity does the term A + W represent in the equation above?
A. The volume of the mixture
B. The mass of fertilizer added
C. The volume of the fertilizer in the mixture
D. The concentration of the fertilizer
2. Two groups of subjects are combined in a psychological research experiment. The mode score for group A is 7 and the mode score for group B is 6. Which of the following conclusions can be made?
A. The mode for the whole group is 6.
B. The mode for the whole group is between 6 and 7.
C. The mode for the whole group is 7.
D. The mode cannot be determined from the given information.
3. The map below shows the layout of streets in a city and the location of several places. Each horizontal or vertical line between two adjacent streets represents a city block, and each city block represents 0.6 miles.
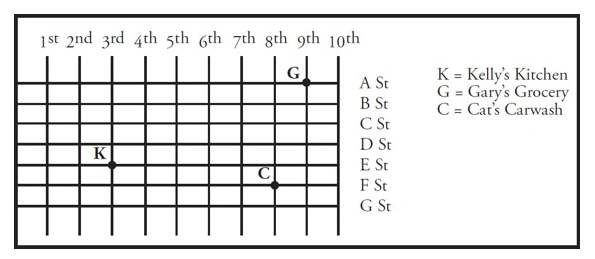
Josh needs to drive from Kelly’s Kitchen to Gary’s Grocery. If Josh drives the shortest distance possible on the roads shown above at a constant speed of 30 miles per hour, how long does it take him to make the trip from Kelly’s Kitchen to Gary’s Grocery?
A. 6 minutes
B. 10 minutes
C. 12 minutes
D. 20 minutes
4. 2s – t = 10
5s = t + 12 – s
Which of the following is a true statement about the system of equations above?
A. There are infinitely many solutions to the system of equations.
B. When the system is solved for s, the result is 5.
C. When the system is solved for t, the result is 6.
D. There are no solutions to the system of equations.
5. The student council at Shermer High School wants to use student opinion to decide on one of three possible homecoming themes for the year. President Peterson thinks that the best way to determine popular opinion is for each of the 10 members of the student council to poll 10 of their friends and select the theme that receives the most votes. Vice President Vaidya wants to go to the cafeteria during lunch and poll 100 students to determine the winner. Treasurer Thompson says the best method would be to assign numbers to each of the 1,000 students in the school, randomly select 100 of them to poll, and select the winner based on the results. Secretary Stephens argues that they must poll each of the 250 members of the senior class to find the most popular theme. Whose method is most likely to accurately determine overall student opinion regarding the most popular homecoming theme?
A. President Peterson
B. Secretary Stephens
C. Treasurer Thompson
D. Vice-President Vaidya