The 2024 SAT standardized test is a critical assessment for college admissions. The math section covers a wide range of topics. To help students prepare, we’ve created a practice paper. This paper includes various math problems to help students become familiar with the test format and excel in their exam.
1. A developer is creating a plan for a 44-acre park that includes a 4-acre lake that cannot be developed. If 8 to 10 acres, inclusive, must be reserved for soccer fields, which of the following inequalities shows all possible values for p, the amount of land that within the park that is available for development?
A. 26 ≤ p ≤ 40
B. 30 ≤ p ≤ 32
C. 34 ≤ p ≤ 36
D. 36 ≤ p ≤ 40
2. Environmentalists have been monitoring the area of a glacier in Canada. The glacier is slowly shrinking. The glacier originally occupied 15,000 square miles, but after two years of monitoring the glacier, the scientists document that the area of the glacier is now 14,910 square miles. If y is the number of years since monitoring began, which equation best describes the glacier’s area, G(y), as a function of time?
A. G(y) = 15,000\( \frac{1}{y} \)
B. G(y) = 15,000 \( (0.003)^y \)y
C. G(y) = 15,000\( (0.997)^y \)
D. G(y) = \( (0.997)^y \)
3. Mike consumes an average of 1,680 calories per day. Each day he has finals, Mike consumes 12% more calories per day than he usually does. During the last day of finals, he celebrates by consuming an additional 900 calories. Which of the following represents the total number of calories Mike consumes during d days of finals?
A. 1.12(1,680d + 900)
B. 1.12(1,680d) + 900
C. 1.12(1,680 + 900)d
D. (1,680 + 0.12d) + 900
4. The varsity swim team at Northwest High is planning a team trip and needs to choose between Austin, TX, and Pensacola, FL. The team takes a vote and the results of the vote are shown in the table below.
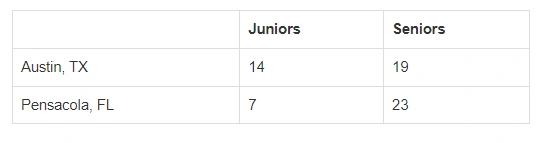
Given the information shown above, which of the following statements is true?
A. The number of juniors that prefer Pensacola, FL, is twice the number of juniors that prefer Austin, TX.
B. The seniors are more than three times as likely to prefer Pensacola, FL, than are the juniors.
C. The number of seniors that prefer Austin, TX, is 5% more than the number of juniors that prefer Austin.
D. One-third of the juniors prefer Pensacola, FL.
5. The 2013 U.S. Census recorded the highest educational attainment of all adults aged 25 years or older in county T, one of the most educated parts of the country. The results are given in the two-way table below.
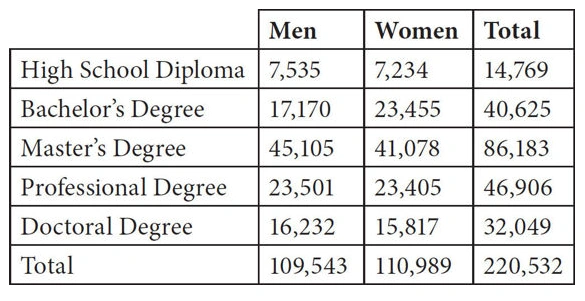
According to the data presented in the table above, if you were to choose a person at random out of the entire population aged 25 years or older in county T, what is the approximate probability that the person you chose is a man with a doctoral degree (given as a percent)?
A. 2%
B. 7%
C. 28%
D. 51%
