2024 SAT Test Math Practice 20

6. If 3y = y + 2, what is the value of 2y ?

A. 1
B. 2
C. 3
D. 4

Correct Answer: B

Answer Explanation:

To solve this question, simply subtract y from both sides of the equation to get 2y = 2, which is (B).

7. Merry joined an online community that charges a monthly fee of $15. A one-time enrollment fee of $50 was charged when she joined. Which of the following represents the total amount of fees that Merry has paid to the community organizers after m months, in dollars?

A. 15m + 50
B. 15 + 50m
C. 15m – 50
D. (15 + 50)m

Correct Answer: A

Answer Explanation:

Whenever the question includes variables, plug in. If m = 2, then Merry would pay the one-time enrollment fee plus 2 months’ worth of monthly fees, which is 50 + 15(2) = 80. Plug in 2 for m in the answer choices to see which answer equals the target number of 80. In (A), 15(2) + 50 = 80. This is the target number, so leave this answer, but be sure to check the other choices just in case. In (B), 15 + 50(2) = 115. In (C), 15(2) – 50 = -20, and in (D), (15 + 50)(2) = 130. Since none of the other answer choices equals the target number, the correct answer is (A).

8. Rob has his favorite guitar tuned up and ready to bring to a performance by his cover band at a local venue Saturday. He decides at the last minute to bring x additional guitars, just in case his favorite guitar has an issue. If the total number of guitars that Robert brings to the performance can be modeled as x + 1, what does the “+ 1” account for in the expression?

A. It accounts for an additional guitar that Rob returns to his house and picks up in the middle of the performance.
B. It accounts for his favorite guitar, which Rob was bringing from the beginning.
C. It accounts for the number of additional guitars that Rob decided to bring.
D. It accounts for an additional non-guitar musical instrument that Rob decided to bring.

Correct Answer: B

Answer Explanation:

Since the question states that Rob is planning to bring his favorite guitar plus x additional guitars, he will have a total of x + 1 guitars. The question states that the variable x represents the number of additional guitars, so the number 1 must represent Rob’s favorite guitar, which is (B).

9. A group of 24 students was polled as to whether they enjoy biology class, chemistry class, both, or neither. The results are shown in the table below:

$Sat math 30 3$

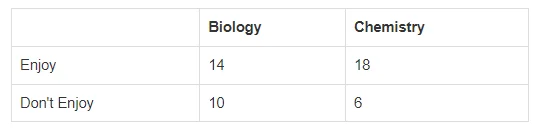
Given the above data, which of the following conclusions is true?

A. The ratio of those who enjoy biology class to those who enjoy chemistry class is 7:8.
B. The ratio of those who enjoy chemistry class to those who don’t enjoy chemistry class is 9:4.
C. The ratio of those who enjoy biology class to those who don’t enjoy chemistry class is 7:2.
D. The ratio of those who don’t enjoy biology class to those who enjoy chemistry class is 5:9.

Correct Answer: D

Answer Explanation:

The best way to approach this question is through POE. According to the data in the table, the ratio of those who enjoy biology to those who enjoy chemistry is 14 to 18, which can be reduced to a ratio of 7 to 9; eliminate (A). The ratio of those who enjoy chemistry to those who don’t enjoy chemistry is 18 to 6, which can be reduced to a ratio of 3 to 1; eliminate (B). The ratio of those who enjoy biology to those who don’t enjoy chemistry is 14 to 6, which can be reduced to a ratio of 7 to 3; eliminate (C). The ratio of those who don’t enjoy biology to those who enjoy chemistry is 10 to 18, which can be reduced to a ratio of 5 to 9; this matches (D).

10. Dr. Goldberg, a noted dietician, mixes different solutions as part of her research into sugar substitutes. By weight, she mixes 40% of a sample of substitute A and 70% of a sample of substitute B to create substitute C. If Dr. Goldberg initially had 60 grams of substitute A and 110 grams of substitute B, then what would be the weight, in grams, of substitute C ?

A. 24
B. 77
C. 101
D. 170

Correct Answer: C

Answer Explanation:

Dr. Goldberg takes 40% of substitute A, which consists of 60 grams. Mathematically, this can be expressed as $ \frac{40}{100} $(60) or (0.4)(60) = 24 grams. She takes 70% of substitute B, which consists of 110 grams. Mathematically, this can be expressed as $ \frac{70}{100} $(110) or (0.7)(110) = 77 grams. Substitute C will therefore consist of 24 grams + 77 grams = 101 grams, which is (C).

Pages: 1 2

< PREVIOUS POST2024 SAT Test Math Practice 19

NEXT POST >2024 SAT Test Math Practice 21

MCQ Question & Answer

Leave A Comment? Click here to cancel reply.