6. Ryan and Allison build a ramp to help their elderly cat, Simms, walk up to their bed. They need the ramp to make a 35° angle with their bedroom floor. How long must the ramp be to reach the top of their bed that is exactly three feet off the ground?
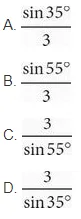
7. If 3a + 2b = 24 and 4a + 5b = 53, what is the value of a + b ?
A. 2
B. 7
C. 9
D. 11
8. Given the equation y = 3x² + 4, what is the function of the coefficient of 3 ?
A. It moves the graph of y = 3x² + 4 three units higher than the graph of y = x² + 4.
B. It moves the graph of y = 3x² + 4 three units lower than the graph of y = x² + 4.
C. It makes the graph of y = 3x² + 4 wider than the graph of y = x² + 4.
D. It makes the graph of y = 3x² + 4 narrower than the graph of y = x² + 4.
9. Steven needs to buy t theme park tickets for himself and his family. Each ticket costs $80, and the number of tickets he needs to buy can be modeled by the expression t² – 4t – 90 = 6 when t > 0. What is the total cost of the theme park tickets that Steven purchased?
A. $640
B. $800
C. $960
D. $1,120
10. 2c + 3d = 17
6c + 5d = 39
In the system of linear equations above, what is the value of 4c – 4d ?
A. -4
B. 1
C. 4
D. 13