6.
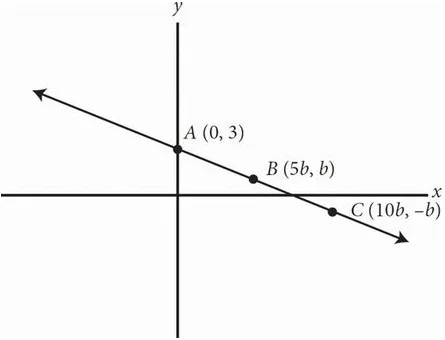
The graph of f(x) is shown above in the xy-plane. The points (0, 3), (5b, b), and (10b, -b) are on the line described by f(x). If b is a positive constant, what are the coordinates of point C ?
A. (5, 1)
B. (10, -1)
C. (15, -0.5)
D. (20, -2)
7. Melanie puts $1,100 in an investment account that she expects will make 5% interest for each three-month period. However, after a year she realizes she was wrong about the interest rate and she has $50 less than she expected. Assuming the interest rate the account earns is constant, which of the following equations expresses the total amount of money, x, she will have after t years using the actual rate?
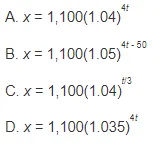
8.
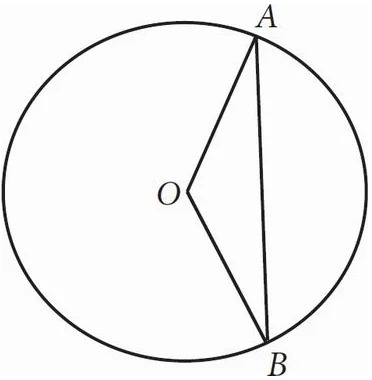
If the radius of the circle above is x, ∠AOB = 120°, and O is the center of the circle, what is the length of chord AB in terms of x ?
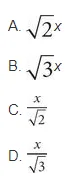
9. The function g is defined by g(x) = 2x² – dx – 6, where d is a constant. If one of the zeros of g is 6, what is the value of the other zero of g ?
A. 2
B. \( \frac{1}{2} \)
C. \( -\frac{1}{2} \)
D. -2
10. The flu shot for a flu season is created from four strains of the flu virus, named Strain A, B, C, and D, respectively. Medical researchers use the following data to determine the effectiveness of the vaccine over the flu season. Table 1 shows the effectiveness of the vaccine against each of these strains individually. The graph below the table shows the prevalence of each of these strains during each month of the flu season, represented as a percentage of the overall cases of flu that month.
For the strain against which the flu shot was the most effective, approximately how effective was the shot overall when that strain was least prevalent?
A. 13%
B. 20%
C. 27%
D. 48%