2024 SAT Test Math Practice 16

6. Jeff tests how the total volume occupied by a fluid contained in a graduated cylinder changes when round marbles of various sizes are added. He found that the total volume occupied by the fluid, V, in cubic centimeters, can be found using the equation below, where x equals the number of identical marbles Jeff added, one at a time, to the cylinder, and r is the radius of one of the marbles. $ V=24π+x(\frac{4}{3}πr³) $. If the volume of the graduated cylinder is 96π cubic centimeters, then, what is the maximum number of marbles with a radius of 3 centimeters that Jeff can add without the volume of the fluid exceeding that of the graduated cylinder?

A. 1
B. 2
C. 3
D. 4

Correct Answer: B

Answer Explanation:

This is a good Plug In the Answers problem. Start with (B) and plug in 2 for x and 3 for r in the equation to get $ V=24π+x(\frac{4}{3}πr³) $, which is equal to the target amount of 96π, so (B) is correct.

7. If b is two more than one-third of c, which of the following expresses the value of c in terms of b ?

$Sat math 25 1$

Correct Answer: C

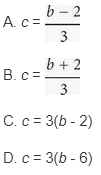
8. The rotation rate of a mixing blade, in rotations per second, slows as a liquid is being added to the mixer. The blade rotates at 1,000 rotations per second when the mixer is empty. The rate at which the blade slows is four rotations per second less than three times the square of the height of the liquid. If h is the height of liquid in the mixer, which of the following represents R(h), the rate of rotation?

A. 4 – 9h²
B. 1,000 – (4 – 3h)
C. 1,000 – (9h – 4)
D. 1,000 – (3h² – 4)

Correct Answer: D

Answer Explanation:

Treat this question as a translation problem. According to the question, R(h) = four rotations per second less than three times the square of the height of the liquid. The height of the liquid is represented by h. Therefore, three times the square of the height of the liquid = 3h². Four less than this amount is 3h² – 4. Since the original speed was 1,000, subtract this value from 1,000 to get the current rate of rotation. The correct answer is (D).

9. A dental hygiene company is creating a new 24-ounce tube of toothpaste by combining its most popular toothpastes, Cavity Crusher and Bad Breath Obliterator. Cavity Crusher contains 0.25% of sodium fluoride as its active ingredient, and Bad Breath Obliterator contains 0.30% of triclosan as its active ingredient for a total of 0.069 ounces of active ingredients in both toothpastes. Solving which of the following systems of equations yields the number of ounces of Cavity Crusher, c, and the number of ounces of Bad Breath Obliterator, b, that are in the new toothpaste?

A. c + b = 0.069
0.25c + 0.3b = 24
B. c + b = 24
0.0025c + 0.003b = 0.069
C. c + b = 24
0.025c + 0.03b = 0.069
D. c + b = 24
0.25c + 0.3b = 0.069

Correct Answer: B

Answer Explanation:

Start with the easier equation and use Process of Elimination. The easier equation is related to the total number of ounces, c + b, in the tube. According to the question, the tube has 24 ounces, so c + b = 24. Eliminate (A), since it does not include this equation. The other equation in the set is related to the amount of active ingredients. According to the question, c includes 0.25% of sodium fluoride and b contains 0.30% triclosan. 0.25% = 0.0025 and 0.30% = 0.003. Therefore, in the correct equation, c should be associated with 0.0025 and b should be associated with 0.003. Eliminate (C) and (D) because both of these equations get the percentages wrong. The correct answer is (B).

10. Which of the following is a possible equation for a circle that is tangent to both the x-axis and the line x = 4 ?

A. (x + 2)² + (y + 2)² = 4
B. (x + 2)² + (y – 2)² = 4
C. (x – 2)² + (y + 4)² = 4
D. (x – 6)² + (y – 2)² = 4

Correct Answer: D

Answer Explanation:

All the answer choices are equal to 4 (which is r², making r = 2), so you need to focus on where the center of the circle lies. If the circle is tangent to both the x axis (which is equivalent to the line y = 0) and the line x = 4, then the center must be 2 units from y = 0 and 2 units from x = 4. Choices (A) and (B) both have centers with an x value of -2 (remember the standard form of the circle equation is (x – h)² + (y – k)² = r², where (h, k) is the center and r is the radius), which is 6 units from x = 4. Eliminate (A) and (B). Choice (C) has a center at (2, -4). The x value is 2 units from x = 4; however, the y value is 4 units from y = 0. Eliminate (C) and choose (D).

Pages: 1 2

< PREVIOUS POST2024 SAT Test Math Practice 15

NEXT POST >2024 SAT Test Math Practice 17

MCQ Question & Answer

Leave A Comment? Click here to cancel reply.