The 2024 SAT standardized test is a critical assessment for college admissions. The math section covers a wide range of topics. To help students prepare, we’ve created a practice paper. This paper includes various math problems to help students become familiar with the test format and excel in their exam.
1.
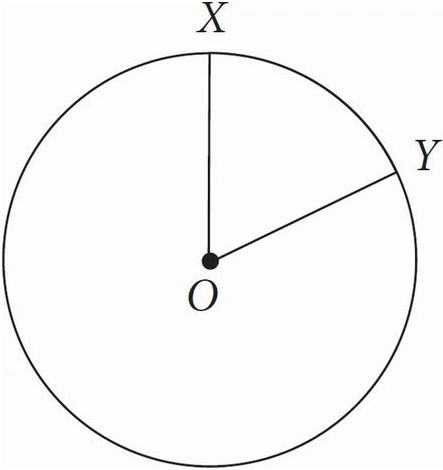
In the figure above, circle O has a radius of 8, and angle XOY measures \( \frac{5}{16}π \) radians. What is the measure of minor arc XY ?
A. \( \frac{5}{16}π \)
B. \( \frac{5}{2}π \)
C. 5π
D. 16π
2.
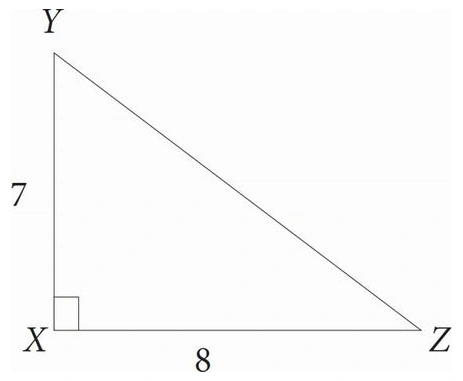
What is the value of tan ∠XZY ?
3.
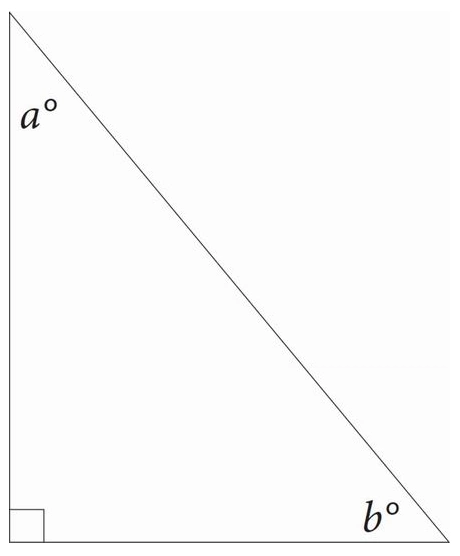
In the figure above, sin a = x. What is the value of cos b?
A. x
B. \( \frac{1}{x} \)
C. |1 – x|
D. \( \frac{90-x}{90} \)
4.
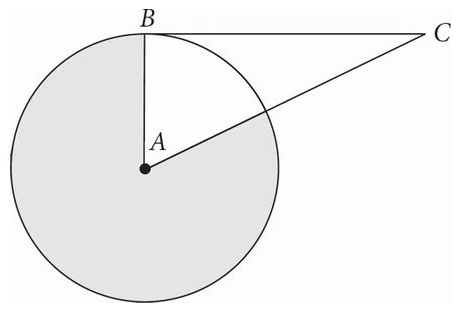
The circle above with center A has an area of 21. BC is tangent to the circle with center A at point B. If AC = 2AB, then what is the area of the shaded region?
A. 3.5
B. 15.75
C. 17.5
D. 21
5. If a rectangular swimming pool has a volume of 16,500 cubic feet, a uniform depth of 10 feet, and a length of 75 feet, what is the width of the pool, in feet?
A. 22
B. 26
C. 32
D. 110
