The 2024 SAT standardized test is a critical assessment for college admissions. The math section covers a wide range of topics. To help students prepare, we’ve created a practice paper. This paper includes various math problems to help students become familiar with the test format and excel in their exam.
1. Marco is ordering salt, which is only sold in 30-pound bags. He currently has 75 pounds of salt, and he needs to have a minimum of 200 pounds. Which of the following inequalities shows all possible values for the number of bags, b, that Marco needs to order to meet his minimum requirement?
A. b ≥ 4
B. b ≥ 5
C. b ≥ 6
D. b ≥ 7
2. A website hopes to sign up 100,000 subscribers. So far, the website has signed up an average of 500 subscribers per day for d days. Which of the following represents the number of additional subscribers, W, the website must sign up to reach its goal?
A. W = 500d
B. W = 99,500d
C. W = 100,000 – 500d
D. W = 100,000 + 500d
3. If f is a function and f(4) = 5, which of the following CANNOT be the definition of f ?
A. f(x) = x + 1
B. f(x) = 2x – 3
C. f(x) = 3x – 2
D. f(x) = 4x – 11
4. Régine is measuring how many solutions from Batch x and Batch y are acidic. She measured a total of 100 solutions from both batches. 40% of the solutions from Batch x and 70% of the solutions from Batch y were acidic, for a total of 48 acidic solutions. Solving which of the following systems of equations yields the number of solutions in Batch x and Batch y ?
A. x + y = 100
0.4x + 0.7y = 48
B. x + y = 48
0.4x + 0.7y = 100
C. x + y = 100 × 2
0.4x + 0.7y = 48
D. x + y = 100
40x + 70y = 48
5.
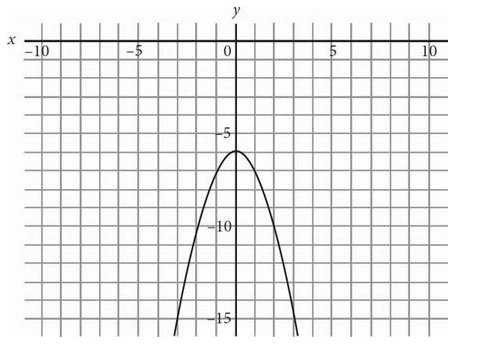
Which of the following equations best describes the figure above?
A. y = \( -x^4 \) + 6
B. y = -(x² + 6)
C. y = -x² + 6
D. y = \( x^4 \) + 6